Michaelis-Menten

A -- B --- C

A reacts with E, and turns into B, with rate constant k₁, which turns into C and regenerates E, with rate constant k₂. Now, B can turn back into A and E, with rate constant k_-1. The Michaelis-Menten mechanism for enzymic catalysis follows this path.

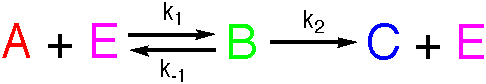
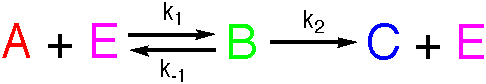
Analytical solutions to the equations for these reactions are not available, but numerical solutions may readily be found. The mechanism may be analysed using the Steady State Approximation to give the following expression for the rate.

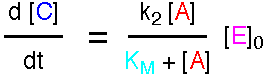
where K_M is called the Michaelis Constant.

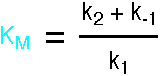
This expression is the Briggs-Haldane analysis of the reaction. The Michaelis-Menten analysis incorporates the additional assumption that k₂ is much less than k_-1, so the Pre-Equilibrium Approximation (see demo3) can be used instead of the Steady State Approximation. This leads to a very similar result, but K_M has the simpler form k_-1/k₁. For a full account, see "Enzyme Structure and Mechanism", A. R. Fersht, 1988, pp98-101.

The rate equation can be integrated in two ways:

Approximation I: Re-introducing the assumption that [E] is small, set [A] = [A]₀ - [C]. The Briggs-Haldane equation can now be integrated:

This works well except at the beginning of the reaction, when [C] and [B] are comparable in size. For this region, it is better to use an alternative approximation.

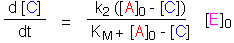
Approximation II: Returning to the unsimplified rate equations, substitute [E] = [E]₀ - [B] and [A] = [A]₀. This will be a good approximation when the amount of product C is small. The equations can now be integrated.

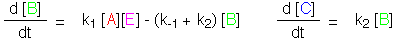
Type:

demo4 k₁ k_-1 k₂ R

to plot the changes in concentrations for systems of this type, calculated numerically. R is the initial ratio of A to E, and so must be between zero and one. The results of both Approximation I and Approximation II are plotted on the graphs. Approximation I works well, except at the beginning of the plot, when the amount of product is much smaller than the amount of starting material. In this initial region, Approximation II is much more effective, and this is the region which is usually of interest in studies of enzyme kinetics.

Examples

demo4 1 0.1 1.1 0.2

This example uses a 4:1 ratio of substrate A to the catalyst E (R = 0.2). This is much more catalyst that is common in an enzymic reaction. However, the Michaelis-Menten analysis (cyan line) gives a very good approximation to the rate of formation of the product C. The systematic error arises because the initial formation of B is not instantaneous, and so the numeric solution (dark blue line) for the formation of C lags behind the Approximation I line. Approximation II (brown line) follows the numeric solution very closely at the start of the reaction.

demo4 1 0.1 1.1 0.5

A stoichiometric amount of catalyst E is used in this example. The Both approximations give a reasonable description of the result, in the regions for which they are valid.

demo4 15 3 19 0.1

With a 9:1 ratio of substrate A to the catalyst E, the Approximation I line falls on top of the more exact solution.

These graphs were created using Gnuplot