|
A problem that has long interested chemists
has been to calculate the number of isomers for an alkane of any given carbon
content. Whilst there appears to be no simple mathematical relationship between
the number of isomers and the carbon content, it is possible to calculate this
number iteratively counting the number of isomers of each fragment into which
the alkane can be decomposed. This approach has been encoded into an algorithm
for calculating the number of isomers of large alkanes - It is estimated that
C167H336 has more isomers than the universe has particles!
We have shown that in fact not all
structural isomers are possible - high level ab initio calculations
show that the C16 and C17 fragments below, if they were synthesized, would be
unstable and rapidly undergo homolytic dissociation at room temperature. Certainly
C17 cannot be made, and it is likely that C16 can only exist at very low temperatures
for a short time.
| 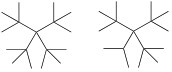
The smallest alkanes which cannot
be made, C17 and C16 |
This factor has been taken into account
in the development of IsoCount which disallows the unstable substructures. The
Applet calculates the number of isomers removing any containing the C17 substructure,
or using the more stringent condition of removing the C16 substructure. The java source code is available.
Robert S. Paton and Jonathan M. Goodman
- Exploration of the Accessible Chemical Space of Acyclic Alkanes
- R. S. Paton and J. M. Goodman J. Chem. Inf. Model. 2007, 47, 2124-2132.
- DOI: 10.1021/ci700246b
- What Is the Smallest Saturated Acyclic Alkane that Cannot Be Made?
- K. M. N. de Silva and J. M. Goodman J. Chem. Inf. Model. 2005, 45, 81-87.
- DOI: 10.1021/ci0497657
- What is the Longest Unbranched Alkane with a Linear Global Minimum Conformation?
- J. M. Goodman J. Chem. Inf. Comput. Sci. 1997, 37, 876-878.
- DOI: 10.1021/ci9704219
This analysis has implications for the synthesis of dendrimers.
|