A two-step reaction

A -- B --- C

A turns into B, with rate constant k₁, which turns into C, with rate constant k₂. Now, B can turn back into A, with rate constant k_-1. The previous example showed the result of k_-1 = 0.

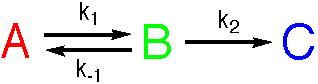
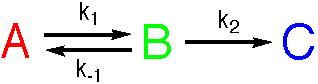
Analytical solutions to the equations for these reactions are not available, but numerical solutions may readily be found. The Steady State Approximation and the Pre-Equilibrium Approximation are often used to analyse systems of this type.

Type:

demo3 k₁ k_-1 k₂

to plot the changes in concentrations for systems of this type, calculated numerically.

demo3ssa k₁ k_-1 k₂
demo3pea k₁ k_-1 k₂
demo3comp k₁ k_-1 k₂

give the results for the Steady State Approximation and the Pre-Equilibrium Approximation, respectively. demo3comp plots the results for the numerical solutions to the differential equations and the formation of C according to both approximations, on the same graph.

Examples

demo3comp 0.2 1 1.1

The concentration of B is always low, so the Steady State Approximation (magenta line) works well. The Pre-Equilibrium Approximation (cyan line) does not. The red, green and blue lines show the concentrations of A, B and C, respectively, as the reaction proceeds, found by numerically solving the differential equations for the reaction. The changes in A and B using the two approximations can be seen by typing: demo3ssa 0.2 1 1.1 and demo3pea 0.2 1 1.1.

demo3comp 1.1 1 0.1

In this example, A and B rapidly reach equilibrium, so the Pre-Equilibrium Approximation (cyan line) works much better than the Steady State Approximation (magenta line). The difference between the numerical solution and the Pre-Equilibrium Approximation occurs at the beginning, whilst A and B attain equilibrium.

demo3comp 1 1.1 1.2

In this example, the concentration of B is not constant, and A and B do not come close to reaching an equilibrium. Neither approximation works very well.

These graphs were created using Gnuplot

Next Example