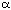 -pinene derived
chiral ligands on the boron (Scheme 1).
This is not predicted by the computational model, and so our previous papers have
only applied the model to E and Z enol borinates.
-pinene derived
chiral ligands on the boron (Scheme 1).
This is not predicted by the computational model, and so our previous papers have
only applied the model to E and Z enol borinates.
Anna Bernardi,(a) Cesare Gennari,(a) Jonathan M. Goodman,*(b) and Ian Paterson (b)
(a) Dipartimento di Chimica Organica e Industriale,
Universita' di Milano, via Venezian 21, 20133 Milano, Italy
(b) University Chemical Laboratory, Lensfield Road,
Cambridge CB2 1EW, England
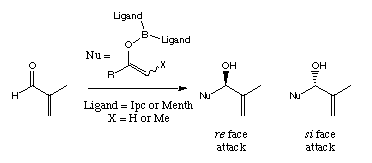
Summary: Force fields have been used to analyse and predict selectivity in the aldol reactions of E and Z enol borinates derived from ethyl ketones. The model is now extended to the boron-mediated aldol reactions of methyl ketones. The correlation between calculation and experiment is good, for achiral substrates and chiral ligands on boron, with the experimentally observed reversal in stereoselectivity for isopinocampheyl ligands being reproduced. Trends in selectivity with different substrates are also calculated correctly.
 -pinene
-pinene
We have been puzzled, however,
by the behaviour of enol borinates derived from methyl ketones, which show a
reversal in stereoselectivity[3] when reacted
with  -pinene derived
chiral ligands on the boron (Scheme 1).
This is not predicted by the computational model, and so our previous papers have
only applied the model to E and Z enol borinates.
-pinene derived
chiral ligands on the boron (Scheme 1).
This is not predicted by the computational model, and so our previous papers have
only applied the model to E and Z enol borinates.
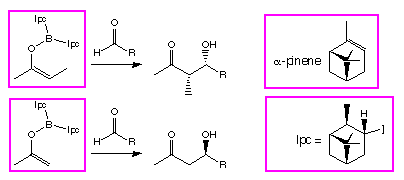
Scheme 1: The reversal in stereoselectivity between methyl and ethyl ketones for  -pinene derived ligands (Ipc).
-pinene derived ligands (Ipc).
The model was used to design a new ligand for the asymmetric aldol reaction, derived from
menthone (Scheme 2) [7].
This new reagent was stereoselective for the aldol reactions of E enol borinates, as we had
hoped, and did not show the reversal in aldehyde
 -face selectivity for methyl ketones.
-face selectivity for methyl ketones.
Our original paper [5] had investigated whether or not there was a correlation between enol borinate conformation
and the sense of asymmetric induction.
This approach did not account for the observed reverse in stereoselectivity.
Inspection of the three dimensional structures of the enol borinates, which
can be obtained by clicking on Scheme 1 and
Scheme 2, shows that the enol borinate
geometry for methyl ketones is reversed, relative to Z enol borinates
for menthone, and not for  -pinene derived ligands. This confirms
that enol borinate geometry is not a useful guide to aldol stereoselectivity.
Recent calculations on the
analogous aza-aldol reaction,[4] however, have
suggested an explanation for this puzzling reversal in selectivity.
There is a bad steric interaction, which is highlighted on this
WWW page
by transparent yellow spheres. The picture is linked to a three dimensional structure.
Inspired by the aza-aldol results, we further investigated the methyl ketone reaction, and in this paper we demonstrate that our computational model can be extended to a
range of methyl ketone aldol reactions, by the introduction of one additional
assumption.
-pinene derived ligands. This confirms
that enol borinate geometry is not a useful guide to aldol stereoselectivity.
Recent calculations on the
analogous aza-aldol reaction,[4] however, have
suggested an explanation for this puzzling reversal in selectivity.
There is a bad steric interaction, which is highlighted on this
WWW page
by transparent yellow spheres. The picture is linked to a three dimensional structure.
Inspired by the aza-aldol results, we further investigated the methyl ketone reaction, and in this paper we demonstrate that our computational model can be extended to a
range of methyl ketone aldol reactions, by the introduction of one additional
assumption.
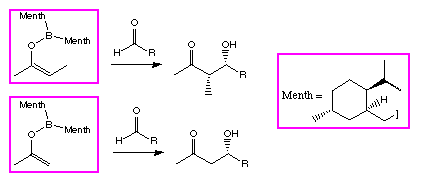
Scheme 2: The lack of reversal in stereoselectivity for the menthone derived ligand
Click inside any of the magenta boxes to get a three dimensional picture of the structure that it contains.
Our analysis of the selectivity of Z and E enol borinates led us to the conclusion that the chair transition structure played an important role in determining the selectivity of the reaction. A force field was developed which predicted the selectivity of the aldol, for these cases. Unfortunately, our model could not predict the selectivity of the analogous methyl ketone reaction. Studies of the aza-aldol reaction [4] suggested that the force field may over-emphasise the importance of the chair transition structure.
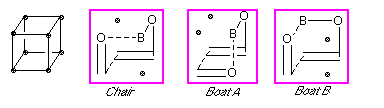
Figure 2: Schematic representations of the three possible transition structures for the boron-mediated aldol
Click on the
Chair,
BoatA or
BoatB
for a three dimensional image of each calculated structure
One solution to this problem would be to rewrite the entire transition state force field. However, the force field had been constructed at the expense of enormous effort, and its final form could not be readily adjusted without losing all the useful results which have been accumulated through its use. Therefore, we considered ways of modifying the procedure, so we might be able to calculate the stereoselectivity of the boron-mediated aldol reactions of methyl ketones, without losing our earlier results.
The force field is based on Allinger's MM2,[6] which provides a reliable framework, but limits the options available to the force field developer. Rather than trying to redesign the force field from scratch, we decided to add a simple filter to the existing force field. The conformation search was performed as before, but all the Chair and Boat B structures that were generated were discarded. This was accomplished in a straightforward way using Clark Still's MacroModel, [8] which can filter structures based on their geometry.
This filtering process is the simplest method of emphasising the importance of the boat transition structures. It may be that an improved force field, perhaps incorporating a different form of the potential function,[9] would be able to model all the different forms of the boron-mediated aldol reaction, without this filtering process. However, we are interested in producing useful tools for organic chemists as rapidly as possible, and this filtering approach enabled us to obtain such a tool very quickly.
The new protocol accounts for the reversal in selectivity observed in changing from Z enol borinates to unsubstituted enol borinates. It also mirrors the trends in changing the size of the group opposite to the side of enolisation. It appears to be a useful tool, therefore, for the chiral ligands that have been tested.
| entry | ketone | ligand | experimental re:si | calculated re:si | structures |
|---|---|---|---|---|---|
| 1 | butanone (Z enol) [2(a)] | Ipc | 1 : 10 | 1 : 19 | |
| 2 | acetone | Ipc | 5.3 : 1 | 1.9 : 1 | good : bad |
| 3 | 3-methyl-butanone | Ipc | 4.9 : 1 | 1.7 : 1 | good : bad |
| 4 | 3,3-dimethyl-butanone | Ipc | 1.4 : 1 | 1.5 : 1 | good : bad |
| 5 | butanone (E enol) [7] | Menth | 7 : 1 | 22 : 1 | |
| 6 | acetone | Menth | 3.9 : 1 | 3.2 : 1 | good : bad |
| 7 | 3-methyl-butanone | Menth | 7.3 : 1 | 6.5 : 1 | good : bad |
| 8 | 3,3-dimethyl-butanone | Menth | 7.1 : 1 | 8.2 : 1 | good : bad |
If this table is not clear, it may be your browser does not interpret the format in the same way as Netscape 1.1N. Click here for an alternative version of Table 1
These observations may be qualitatively explained by Figure 3. The smallest group of the ligand (hydrogen) points into the centre of the boat, the most sterically crowded direction. The next most important interaction is with the aldehyde's hydrogen, which points towards the ligand. The medium group will, therefore, point in this direction. As the alkyl group on the ketone (R) gets larger, the interaction with the second ligand becomes more important, and this affects the selectivity.
This analysis appears to fit the results from the 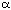 -pinene derived
chiral ligands quite well. The menthone derived ligand, however, is much harder to analyse in
terms of large, medium and small groups. It is clear from the structures that the two ligands
interact strongly with each other. The 'open' position for the ligand appears to interact with the R-group as well as the aldehyde hydrogen.
It is hard to fit these observations into a scheme such as Figure 3. If we knew that the computational mode was an accurate representation of
physical reality, then it would be reasonable simply to trust it. As we have no such assurance,
all conclusions that are drawn from the model must be treated with caution.
-pinene derived
chiral ligands quite well. The menthone derived ligand, however, is much harder to analyse in
terms of large, medium and small groups. It is clear from the structures that the two ligands
interact strongly with each other. The 'open' position for the ligand appears to interact with the R-group as well as the aldehyde hydrogen.
It is hard to fit these observations into a scheme such as Figure 3. If we knew that the computational mode was an accurate representation of
physical reality, then it would be reasonable simply to trust it. As we have no such assurance,
all conclusions that are drawn from the model must be treated with caution.
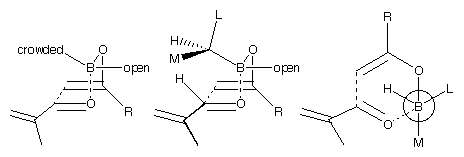
Figure 3: Different views of the boat transition structure
The introduction of an assumption about the transition structure of the boron-mediated aldol reaction of methyl ketones allows us to account for the selectivity of the reactions. The calculations do not prove that the aldol reaction of methyl ketones goes through a boat transition structure, but do show that experimental results can be rationalised by making this assumption.
We can predict the behaviour of E and Z enol borinates derived from ethyl ketones as well as the unsubstituted enol borinates from methyl ketones, using a computational model. The calculations appear to be accurate enough to account for the face of attack on an aldehyde. The precision is severely tested, however, if the reaction has several competing chiral components (multiple asymmetric induction).
Acknowledgments: Financial support from NATO (Collaborative Grant 0368/88), The Commission of the European Community (H.C.M. Network Grant n. ERB CHR XCT 930141), the Royal Society (JMG) and the Cambridge Centre for Molecular Recognition is gratefully acknowledged.
(1)
Kim, B. M.; Williams, S. F.; Masamune, S. Comprehensive Organic Synthesis, ed. Trost, B. M.; Fleming, I. Pergamon Press, Oxford 1991, 2, 239
(2)
(a) Bernardi, A.; Capelli, A. M.; Gennari, C.; Goodman, J. M.; Paterson, I. J. Org. Chem. 1990, 55, 3576.
(b) Bernardi, A.; Capelli, A. M.; Comotti, A.; Gennari, C.; Gardner, M.; Goodman, J. M.; Paterson, I. Tetrahedron 1991, 47, 3471.
(c) Gennari, C.; Vieth, S.; Comotti, A.; Vulpetti, A.; Goodman, J. M.; Paterson, I. Tetrahedron 1992, 48, 4439.
(d) Bernardi, A.; Cassinari, A.; Comotti, A.; Gardner, M.; Gennari, C.; Goodman, J. M.; Paterson, I. Tetrahedron 1992, 48, 4183.
(e) Vulpetti, A.; Bernardi, A.; Gennari, C.; Goodman, J. M.; Paterson, I. Tetrahedron 1993, 49, 685.
(f) Bernardi, A.; Comotti, A.; Gennari, C.; Hewkin, C. T.; Goodman, J. M.; Schlapbach, A.; Paterson, I. Tetrahedron 1994, 50, 1227.
(3)
Paterson, I.; Goodman, J. M.; Lister, M. A.; Schumann, R. C.; McClure, C.
K.; Norcross. R. D. Tetrahedron 1990, 46, 4663.
(4)
Bernardi, A.; Gennari, C; Goodman, J. M.; Leue, V.; Paterson, I. Tetrahedron 1995, 51, 4853.
(5)
Goodman, J. M.; Kahn, S. D.; Paterson, I. J. Org. Chem. 1990, 55, 3295.
(6)
Allinger, N. L. J. Am. Chem. Soc. 1977, 99, 8127.
(7)
Gennari, C.; Hewkin, C. T.; Molinari, F.; Bernardi, A.; Comotti
, A.; Goodman, J. M.; Paterson, I. J. Org. Chem. 1992, 57,
5173.
(8)
Mohamadi, F.; Richards, N. G. J.; Guida, W. C.; Liskamp, R.; Lipton, M .; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W. C. J.Comp.Chem. 1990, 11, 440.
(9)
Vinter, J. G. J. Comp.-Aided Mol. Design 1994, 8, 653.
entry ketone ligand experimental calculated
re:si re:si
(1) butanone (Z enol)[2(a)] Ipc 1 : 10 1 : 19
(2) acetone Ipc 5.3 : 1 1.9 : 1
(3) 3-methyl-butanone Ipc 4.9 : 1 1.7 : 1
(4) 3,3-dimethyl-butanone Ipc 1.4 : 1 1.5 : 1
(5) butanone (E enol) [7] Menth 7 : 1 22 : 1
(6) acetone Menth 3.9 : 1 3.2 : 1
(7) 3-methyl-butanone Menth 7.3 : 1 6.5 : 1
(8) 3,3-dimethyl-butanone Menth 7.1 : 1 8.2 : 1
If you still cannot read the table, click here for a picture of it.