Consecutive first step reversible reactions
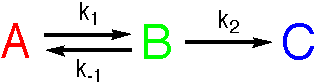
A turns into B, with rate constant k1, which
turns into C, with rate constant k2. Now,
B can turn back into A, with rate constant k-1.
The problem of integrating the rate equations can be overcome by the use of approximations
(P. W. Atkins, Physical Chemistry, Oxford University Press). An important approach is the
Steady-State Approximation that assumes that the concentration of B does not alter.
This simplification leads to analytical solutions to the rate equations.
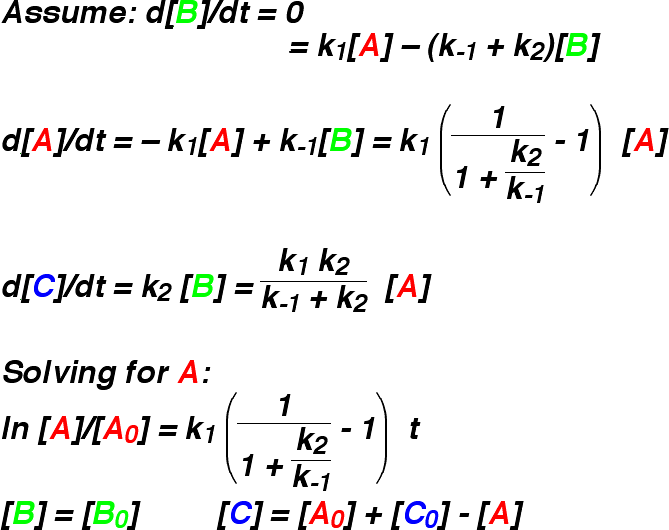
How good is this approximation? This question has been discussed before,
(Pavlis, R. R. J. Chem. Educ. 1997, 74, 1139; Viossat, V.;
Ben-Aim, R. I. J. Chem. Educ. 1993, 70, 732.) and can be
analysed using a variety of programs. A Java applet
to do this is available on http://www-jmg.ch.cam.ac.uk/tools/magnus/kinetic.html.
The approximation will be best if the concentration of B stays approximately
constant, which means that the sum of k-1 and k2
must be greater than k1 if the initial concentration of B is zero, and
it must be equal to k1 if the initial concentration is not zero. This seems a
stringent test. The applet makes the comparison in a visual way. The figure shows the
changes in concentration of A, B, and C as the reaction proceeds, with
k1 = 1.5, k-1 = 1.0, and k2 = 0.1.
This is a very bad case for the steady state approximation, as the rate constant for
the formation of B is greater than the rate constants for its destruction. As a result,
the concentration of B builds up as the reaction proceeds, before eventually
draining into C. The steady state approximation assumes that the concentration of
B does not change, and so it stays at its initial concentration of zero. This gives a very
different reaction profile. Experimentation with the applet shows that the approximation
works well if k1 is smaller than k-1 and k2
as expected. How much smaller do they need to be? Can one be larger and the other smaller?
The answer can be found by adjusting the settings of the applet.
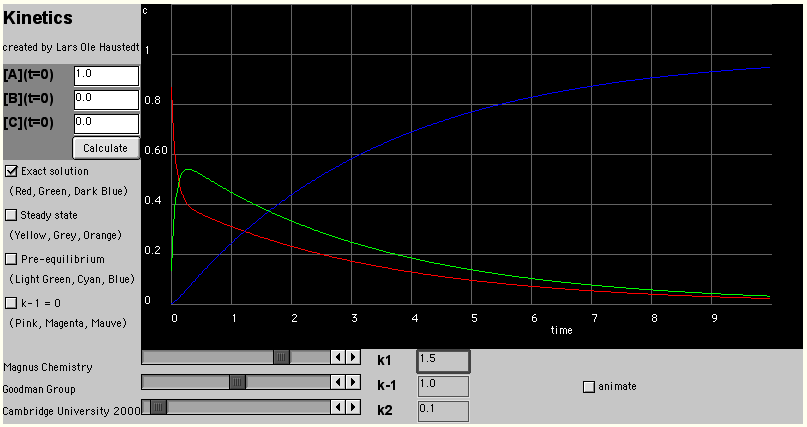
An alternative approach to solving the rate equations is to use the Pre-equilibrium
Approximation. This is that A and B are always present in their equilibrium ratios, which is
equivalent to assuming that k2 is much slower than both k1
and k-1.
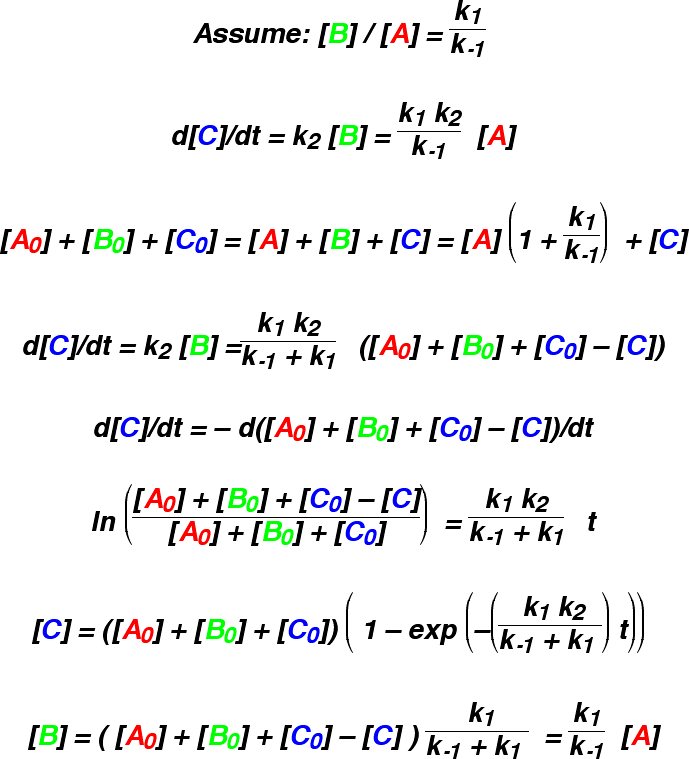
The applet also draws the results of making this assumption. A and B immediately
change from their initial concentrations to the equilibrium concentrations, and then both
gradually diminish as C forms. This works best if k1 and k-1
are fast, and the applet helps to answer the question: how fast? The approximation is poor at
the beginning of the reaction, as A and B reach equilibrium too fast. However, it often traces
the rest of the reaction quite well.
Neither of these approximations reproduces the gradual increase and decrease in
the concentration of B that occurs for may choices of k1, k-1
and k2. Another approximation is to assume that k-1 is zero. This may appear
a drastic approximation, but it leads to rate equations which can be solved analytically.
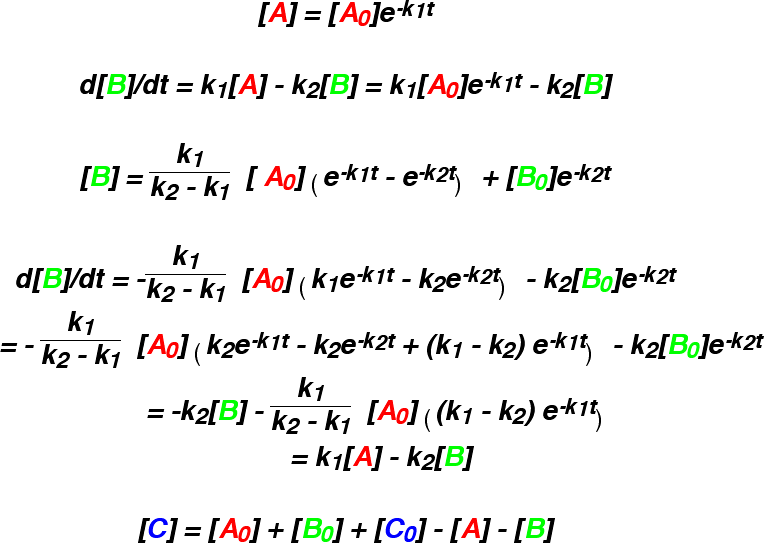
This approximation gives curves which are of the same general form as the numeric
results. If k-1 is zero, then the numeric and analytical solutions coincide.
However, if k-1 is not zero, B forms too quickly.
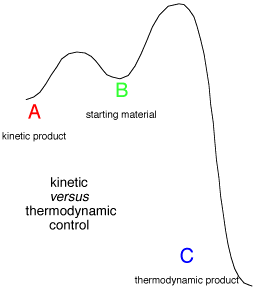
The same applet may also be used to investigate thermodynamic and kinetic control.
If the initial conditions are set so that A and C have a concentration of zero, and B has a
concentration of one, then the equations correspond to a common situation where a starting
material may react to form a kinetically favoured product, or a different thermodynamically
favoured product.
How long will it take to get the maximum yield of the kinetic product? At what point
will the thermodynamic product become the main component of the mixture? These
questions can be answered by adjusting the parameters of the applet
This applet allows students
to explore the effect of various kinetic regimes, by displaying the solutions of rate
equations, solved by numerical means, and comparing them with the results of various approximations.
|