Michaelis-Menten
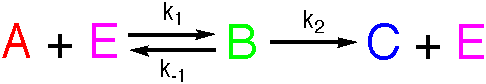
A reacts with E, and turns into B, with rate constant k1,
which turns into C and regenerates E, with rate constant k2.
Now, B can turn back into A and E, with rate constant k-1. The
Michaelis-Menten mechanism for enzymic catalysis follows this path.
Analytical solutions to the equations for these reactions are not available,
but numerical solutions may readily be found. The mechanism may be analysed
using the Steady State Approximation to give the following expression
for the rate.
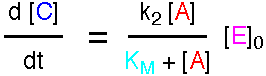
where KM is called the Michaelis Constant.
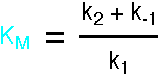
This expression is the Briggs-Haldane analysis of the reaction.
The Michaelis-Menten analysis incorporates the additional assumption that
k2 is much less than k-1, so the Pre-Equilibrium
Approximation can be used instead of the Steady State Approximation. This leads
to a very similar result, but KM has the simpler form k-1/k1.
For a full account, see "Enzyme Structure and Mechanism", A.
R. Fersht, 1988,
pp98-101.
The rate equation can be integrated in two ways:
Approximation I: Re-introducing the assumption that [E] is small,
set [A] = [A]0 - [C]. The Briggs-Haldane equation can
now be integrated:
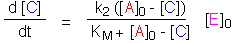
This works well except at the beginning of the reaction, when [C] and [B]
are comparable in size. For this region, it is better to use an alternative
approximation.
Approximation II: Returning to the unsimplified rate equations,
substitute [E] = [E]0 - [B] and [A] = [A]0. This
will be a good approximation when the amount of product C is small. The
equations can now be integrated.
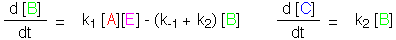
The Applet below demonstartes these two approximations.
Approximation
I works well, except at the beginning of the plot, when the amount
of product is much smaller than the amount of starting material. In this
initial region, Approximation II is much more effective, and this
is the region which is usually of interest in studies of enzyme kinetics.
|